九九のきまり

３×４について考えてみよう

かけ算の交換法則（こうかんほうそく）

「３×４」の ３をかけられる数 ４をかける数というよ。そして、かけ算では「かけられる数」と「かける数」を入れかえても、同じ答えになるんだ。

「３×４」と「４×３」は、同じ答えということだね。

これを しきで書くとこうなるよ。

３×４ ＝ ４×３

かける数が１大きくなると…

「３×４」は「３が４こ」。
これを たし算に直すと「３＋３＋３＋３」。

「３×５」は「３が５こ」。
これを たし算に直すと「３＋３＋３＋３＋３」。

つまり「３×５」は「３×４」よりも、３大きいんだ。

このように、九九では かける数が１つ大きくなったり １つ小さくなると、答えが「かけられる数」のぶん、大きくなったり 小さくなったりするよ。

「３×５」は「３×４ ＋ ３」ということだね。

これを しきで書くとこうなるよ。

３×５ ＝ ３×４ ＋ ３

もしくは、こんなふうにも書ける

３×４ ＝ ３×５ − ３

かけ算の工夫（くふう）

１×１ 〜 ９×９までの九九は おぼえていても、それより大きな数のかけ算では こまってしまうよね？

そんな時は、考えかたを 工夫してみよう。

下の図でわかるかな？ たとえば「３×１4」は「３×９ と ３×５」に分けることができるよ。

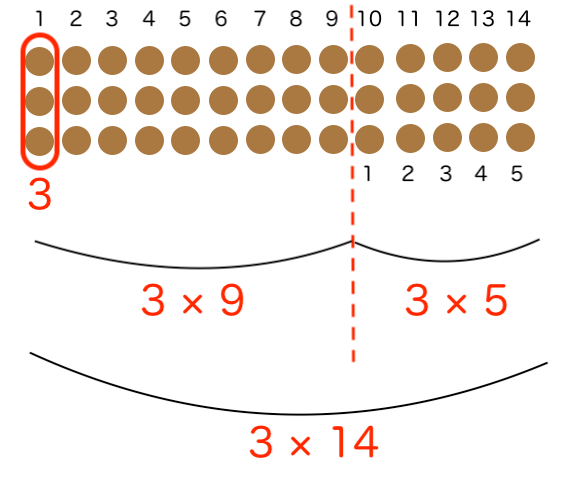
これを しきで書くとこうなるよ。

３×14 ＝ ３×９ ＋ ３×５

たし算・ひき算・かけ算・わり算が まじったしきでは、かけ算・わり算を先に計算することに ちゅういしよう。

上のしきの右がわ「３×９ ＋ ３×５」は、「27 ＋ 15」となって、答えは42。

このように、３×14を そのまま計算できなくても、3のだんの九九を知っていれば、答えを もとめることができるんだ。